ac

Tarjan算法与并查集解决批量查询【在二叉树中找到两个节点的最近公共祖先】

query:
4 (7
7 (8
2 (8 9
         1
      /     \
     2        3
    / \        \
   4  5         6
     / \       /
    7   8     9

遍历到4，发现有7,但是7没有遍历到

遍历到2，{2} 和 {4} 结合{2, 4} fa为 2

{5, 7} fa为 5

{5, 7, 8} fa为 5

{2, 4, 5, 7, 8} 祖先为2

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Map;
import java.util.Scanner;

class TreeNode{
    TreeNode left;
    TreeNode right;
    int val;

    public TreeNode(int val) {
        this.val = val;
        left = null;
        right = null;
    }
}

class Query{
    TreeNode o1;
    TreeNode o2;

    public Query(TreeNode o1, TreeNode o2) {
        this.o1 = o1;
        this.o2 = o2;
    }
}

class DisjointSets{
    Map<TreeNode, TreeNode> fatherMap;// 存根
    Map<TreeNode, Integer> rankMap; // 秩

    public DisjointSets() {
        this.fatherMap = new HashMap<>();
        this.rankMap = new HashMap<>();
    }

    void makeSets(TreeNode head){
        fatherMap.clear();
        rankMap.clear();
        preOrderMake(head);
    }

    void preOrderMake(TreeNode head){
        if(head == null){
            return;
        }
        // 根都是自己,秩都是0
        fatherMap.put(head, head);
        rankMap.put(head, 0);
        preOrderMake(head.left);
        preOrderMake(head.right);
    }

    public TreeNode findFa(TreeNode n){
        TreeNode fa = fatherMap.get(n);
        if(fa != n){
            fa = findFa(fa);
        }
        fatherMap.put(n, fa);
        return fa;
    }

    public void union(TreeNode a, TreeNode b){
       if(a == null || b == null){
           return;
       }
       TreeNode aFa = findFa(a);
       TreeNode bFa = findFa(b);
       if(aFa != bFa){
           int aRank = rankMap.get(aFa);
           int bRank = rankMap.get(bFa);
           if(aRank < bRank){
               fatherMap.put(aFa, bFa); // aFa 接到 bFa下面，bFa作为父根，即秩大的作为根
           }else if(aRank > bRank){
               fatherMap.put(bFa, aFa);
           }else {
               fatherMap.put(bFa, aFa);
               rankMap.put(aFa, aRank + 1);
           }
       }
    }
}

class TarJan{
    Map<TreeNode, LinkedList<TreeNode>> queryMap;
    Map<TreeNode, LinkedList<Integer>> indexMap;
    Map<TreeNode, TreeNode> ancestorMap;
    DisjointSets sets;

    public TarJan() {
        // 临接表，key为查询涉及的某个节点，value是个链表
        queryMap = new HashMap<>();
        // key为查询涉及的某个节点，value是个链表,表示设置的结果位置
        indexMap = new HashMap<>();
        ancestorMap = new HashMap<>();
        sets = new DisjointSets();
    }

    public TreeNode[] query(TreeNode head, Query[] queries){
        TreeNode[] ans = new TreeNode[queries.length];
        setQueries(queries, ans);
        // 初始化并查集
        sets.makeSets(head);
        // 设置结果
        setAnswers(head, ans);
        return ans;
    }

    public void setQueries(Query[] ques, TreeNode[] ans){
        TreeNode o1 = null;
        TreeNode o2 = null;
        for(int i=0;i<ques.length;i++){
            o1 = ques[i].o1;
            o2 = ques[i].o2;
            if(o1 == o2 || o1 == null || o2 == null){
                ans[i] = o1 != null ? o1 : o2;
            }else {
                if(!queryMap.containsKey(o1)){
                    queryMap.put(o1, new LinkedList<>());
                    indexMap.put(o1, new LinkedList<>());
                }
                if(!queryMap.containsKey(o2)){
                    queryMap.put(o2, new LinkedList<>());
                    indexMap.put(o2, new LinkedList<>());
                }
                queryMap.get(o1).add(o2);
                indexMap.get(o1).add(i);
                queryMap.get(o2).add(o1);
                indexMap.get(o2).add(i);
            }
        }
    }

    public void setAnswers(TreeNode head, TreeNode[] ans){
        if(head == null){
            return;
        }
        setAnswers(head.left, ans);
        sets.union(head.left, head);
        ancestorMap.put(sets.findFa(head), head);

        setAnswers(head.right, ans);
        sets.union(head.right, head);
        ancestorMap.put(sets.findFa(head), head);

        // 看查询中是否有有与node相关的，queryMap 和 indexMap 获取
        LinkedList<TreeNode> nList = queryMap.get(head);
        LinkedList<Integer> iList = indexMap.get(head);
        while (nList != null && ! nList.isEmpty()){
            // 取头部元素，求的是 node 和 head 的公共节点
            TreeNode node = nList.poll();
            // 原始 query 的 index
            int index = iList.poll();
            TreeNode nodeFa = sets.findFa(node);
            if(ancestorMap.containsKey(nodeFa)){
                ans[index] = ancestorMap.get(nodeFa);
            }
        }
    }

}


public class Main {
    public static Scanner sc = new Scanner(System.in);

    public static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static long mod = (long) Math.pow(2, 29);

    public static void main(String[] args) throws Exception {
        String line;
        String[] strArr;
        line = reader.readLine();
        strArr = line.split(" ");
        int n = Integer.valueOf(strArr[0]);
        int rootVal = Integer.valueOf(strArr[1]);
        Map<Integer, TreeNode> mp = new HashMap<>(n);
        for (int i = 0; i < n; i++) {
            line = reader.readLine();
            strArr = line.split(" ");
            int val = Integer.valueOf(strArr[0]);
            int leftVal = Integer.valueOf(strArr[1]);
            int rightVal = Integer.valueOf(strArr[2]);

            if (!mp.containsKey(val)) {
                mp.put(val, new TreeNode(val));
            }
            if (leftVal != 0) {
                if (!mp.containsKey(leftVal)) {
                    mp.put(leftVal, new TreeNode(leftVal));
                }
                mp.get(val).left = mp.get(leftVal);
            }
            if (rightVal != 0) {
                if (!mp.containsKey(rightVal)) {
                    mp.put(rightVal, new TreeNode(rightVal));
                }
                mp.get(val).right = mp.get(rightVal);
            }
        }
        TreeNode root = mp.get(rootVal);
        n = Integer.valueOf(reader.readLine());
        Query[] queries = new Query[n];
        for(int i=0;i<n;i++) {
            line = reader.readLine();
            strArr = line.split(" ");
            int p = Integer.valueOf(strArr[0]);
            int q = Integer.valueOf(strArr[1]);
            queries[i] = new Query(mp.get(p), mp.get(q));
        }
        TreeNode[] ans = tarJanQuery(root, queries);
        // 打印结果
        for(int i=0;i<ans.length;i++){
            System.out.println(ans[i].val);
        }
    }

    static TreeNode[] tarJanQuery(TreeNode head, Query[] queries){
        TreeNode[] ans = new TarJan().query(head, queries);
        return ans;
    }

}
/*
         1
      /     \
     2        3
    / \      / \
   4  5     6  7
              /
             8

8 1
1 2 3
2 4 5
4 0 0
5 0 0
3 6 7
6 0 0
7 8 0
8 0 0
4
4 5
5 2
6 8
5 8

2
2
3
1
 */

并查集

66题《并查集的实现》

Tarjan算法

无向图中，从i能到达j，则称i,j连通
如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。
如果有向图G的每两个顶点都强连通，称G是一个强连通图。
有向图的极大强连通子图，称为强连通分量(strongly connected components)。

tarjan算法简单例子图解法

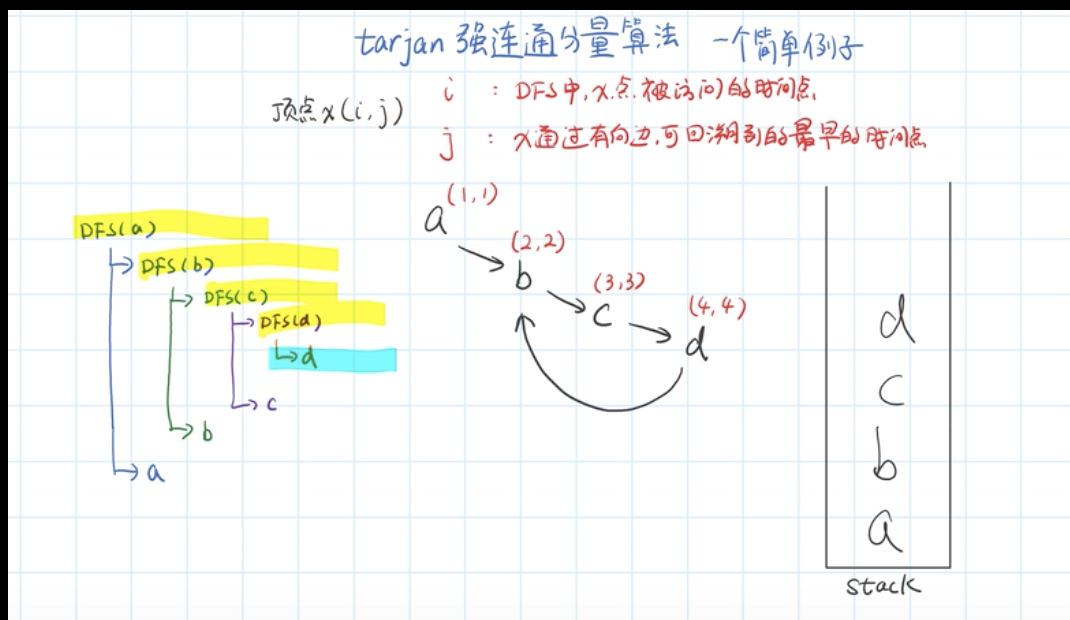
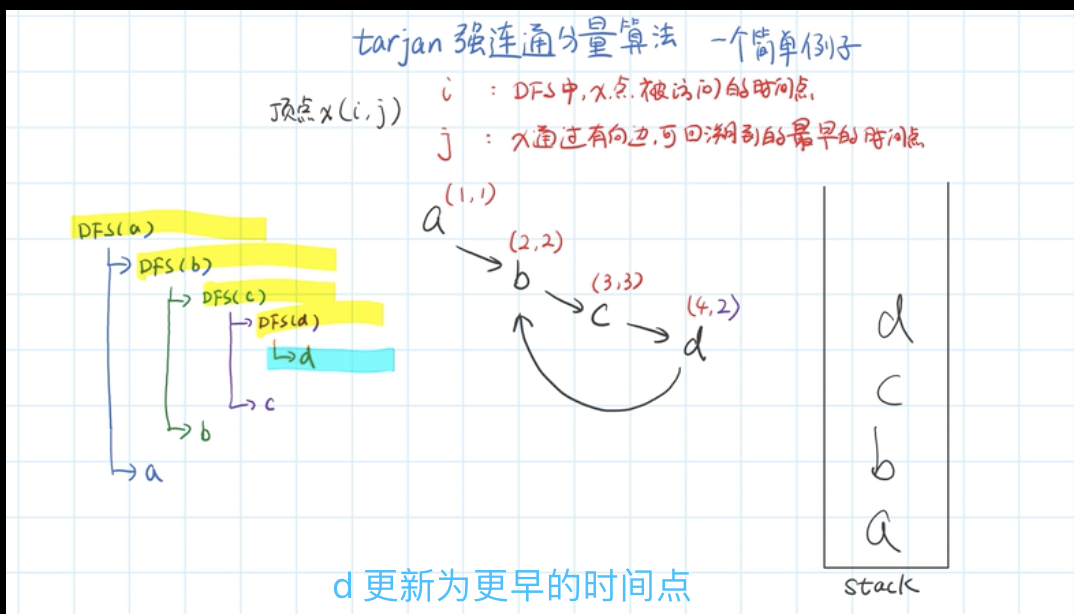
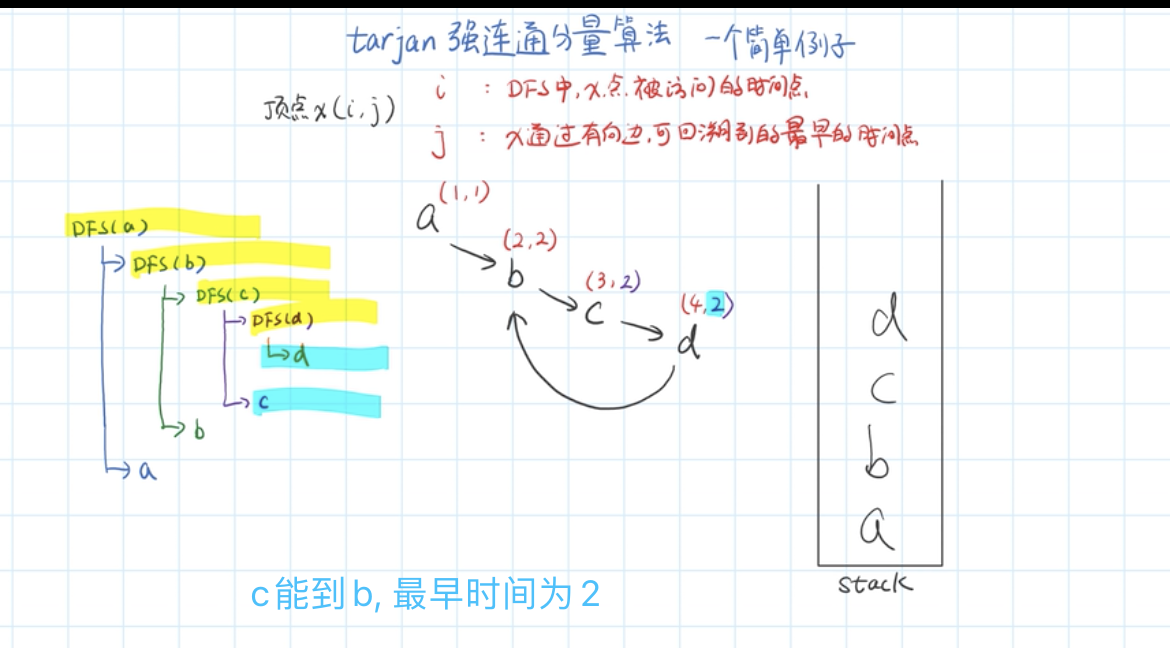
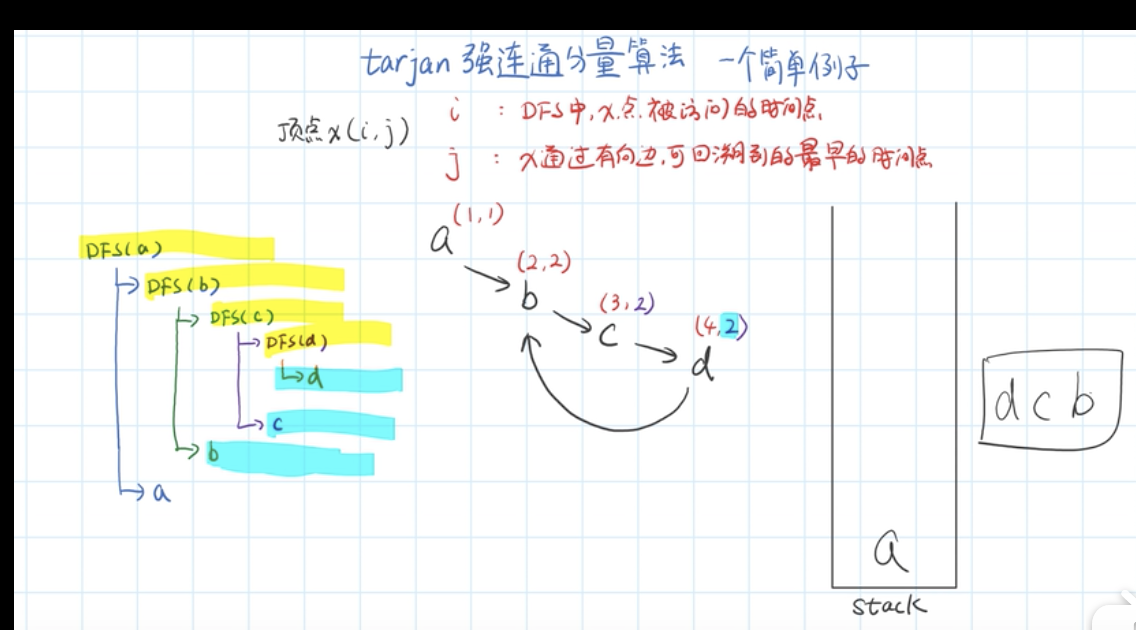
复杂点的

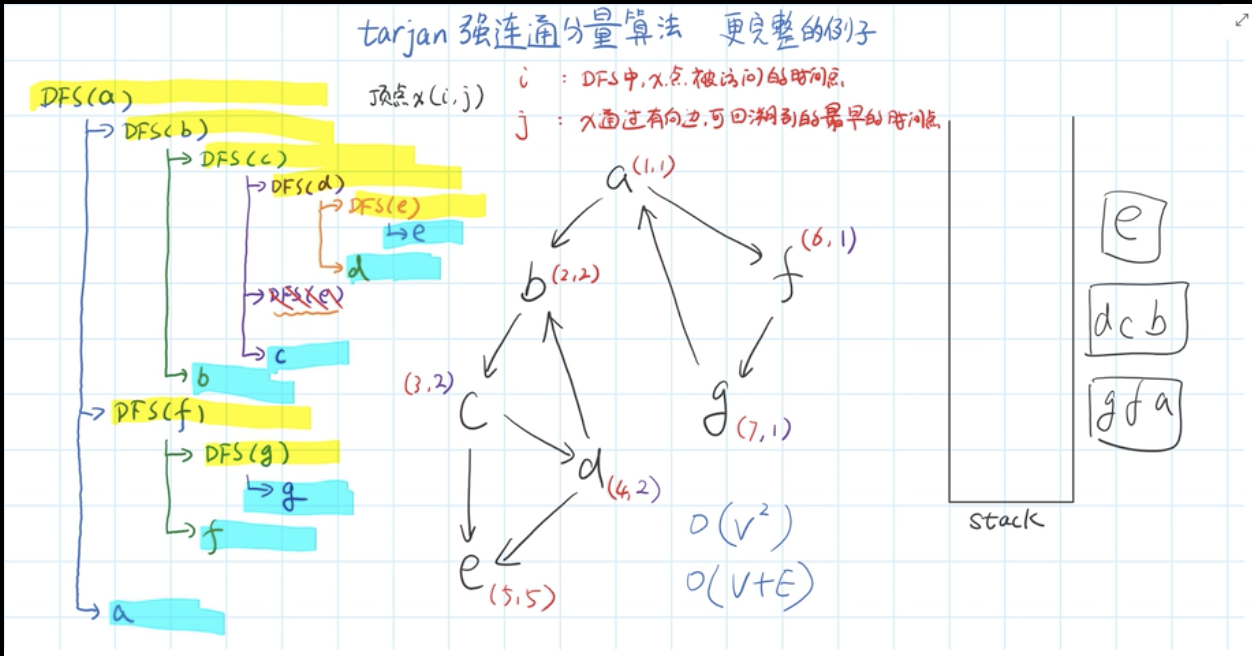
code编码

如下：子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量

1  ------> 3  -----> 5
| ^        |         |
|    \     |         |
|      \   |         |
V        \ V         V
2 -------> 4  -----> 6

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量

dfs方式1: 先输出自己，然后访问与自己相关的点，不断递归（类似先序）
dfs方式2: 访问完与自己相关的点，不断递归，再输出自己（类似后序）

定义DFN(u)为节点u搜索的次序编号(时间戳)，一旦某个点被DFS到后，这个时间戳就不再改变（且每个点只有唯一的时间戳）
定义Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号,Low[ ]相等的点相当于在一个强连通量上
则当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量
初始时：dfn[ ] = low[ ] = ++count

4节点，最早回溯到1，1的次序是dfn[1] = 1, 所以，low[4] = 1

完整code

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;

// 有向边
class Edge{
    boolean inStack; // 是否栈中
    List<Integer> next;
}

public class Main {
    public static Scanner sc = new Scanner(System.in);

    public static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static long mod = (long) Math.pow(2, 29);

    public static int N = 1001;

    static int[] dfn = new int[N];
    static int[] low = new int[N];
    static Edge[] edges = new Edge[N];


    static void add(int u, int v){
        if(edges[u] == null){
            edges[u] = new Edge();
            edges[u].next = new ArrayList<>();
        }
        if(edges[v] == null) {
            edges[v] = new Edge();
            edges[v].next = new ArrayList<>();
        }
        edges[u].next.add(v);
    }

    static Stack<Integer> sta = new Stack<>();
    static int count = 0;

    static void tarjan(int now){
        dfn[now] = low[now] = ++ count;
        sta.push(now);
        edges[now].inStack = true;
        for(Integer v: edges[now].next){
            if(dfn[v] <= 0){ // v 没有被访问过，递归 v
                tarjan(v);
                low[now] = Math.min(low[now], low[v]); // 回溯取最小，v是now的next
            }else if(edges[v].inStack){ // 在栈中, 则取其次序号dfn判断
                low[now] = Math.min(low[now], dfn[v]);
            }
        }
        if(low[now] == dfn[now]){
            int cur;
            do{
                cur = sta.pop();
                edges[cur].inStack = false;
                System.out.print(cur + " ");
            }while (cur != now);
            System.out.println();
        }
    }

    public static void main(String[] args) throws Exception {
        String line;
        String[] strArr;
        line = reader.readLine();
        strArr = line.split(" ");
        int n = Integer.valueOf(strArr[0]);
        int num = Integer.valueOf(strArr[1]);
        for (int i = 0; i < num; i++) {
            line = reader.readLine();
            strArr = line.split(" ");
            int u = Integer.valueOf(strArr[0]);
            int v = Integer.valueOf(strArr[1]);
            add(u, v);
        }
        for(int i=1;i<=n;i++){
            if(edges[i]!= null && edges[i].next != null && ! edges[i].next.isEmpty()) {
                Collections.sort(edges[i].next);
            }
        }
        tarjan(1);
        System.out.println();
    }

}
/*
6 8
1 3
1 2
2 4
3 4
3 5
4 6
4 1
5 6

1  ------> 3  -----> 5
| ^        |         |
|    \     |         |
|      \   |         |
V        \ V         V
2 -------> 4  -----> 6
 */

完整code2

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;

// 有向边
class Edge{
    boolean inStack; // 是否栈中
    List<Integer> next; // 指向的节点
}

public class Main {
    public static Scanner sc = new Scanner(System.in);

    public static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static long mod = (long) Math.pow(2, 29);

    public static int N = 1001;

    static int[] dfn = new int[N];
    static int[] low = new int[N];
    static Edge[] edges = new Edge[N];


    static void add(int u, int v){
        if(edges[u] == null){
            edges[u] = new Edge();
            edges[u].next = new ArrayList<>();
        }
        if(edges[v] == null) {
            edges[v] = new Edge();
            edges[v].next = new ArrayList<>();
        }
        edges[u].next.add(v);
    }

    static Stack<Integer> sta = new Stack<>();
    static int count = 0;

    static void dfs(int now){
        // 访问并入栈
        dfn[now] = low[now] = ++ count;
        sta.push(now);
        edges[now].inStack = true;
        // dfs遍历
        for(Integer v: edges[now].next){
            if(dfn[v] <= 0){ // v 没有被访问过，递归 v
                dfs(v);
                // 回溯，取最小的能回到的low
                low[now] = Math.min(low[now], low[v]);
            }else if(edges[v].inStack){
                // 否则访问的是在栈中的，当前访问的看能否回到栈中最小的
                low[now] = Math.min(low[now], low[v]);
            }
        }
        // 如果dfs 和 low 相等了，表示一个强联通分量构成
        if(low[now] == dfn[now]){
            int cur;
            do{
                cur = sta.pop();
                // 消除inStack, 但是dfs不消除
                edges[cur].inStack = false;
                System.out.print(cur + " ");
            }while (cur != now);
            System.out.println();
        }
    }

    public static void main(String[] args) throws Exception {
        String line;
        String[] strArr;
        line = reader.readLine();
        strArr = line.split(" ");
        int n = Integer.valueOf(strArr[0]);
        int num = Integer.valueOf(strArr[1]);
        for (int i = 0; i < num; i++) {
            line = reader.readLine();
            strArr = line.split(" ");
            int u = Integer.valueOf(strArr[0]);
            int v = Integer.valueOf(strArr[1]);
            add(u, v);
        }
        for(int i=1;i<=n;i++){
            if(edges[i]!= null && edges[i].next != null && ! edges[i].next.isEmpty()) {
                Collections.sort(edges[i].next);
            }
        }
        dfs(1);
        System.out.println();
    }

}
/*
6 8
1 3
1 2
2 4
3 4
3 5
4 6
4 1
5 6

6
5
3 4 2 1
 */